| |
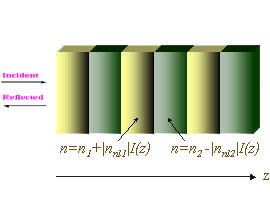 Photonic band-gap crystals are periodic optical materials, spectrum of which consists of bands, separated
by band gaps. Periodic and nonlinear properties of the photonic crystals are modeled with the nonlinear
Maxwell equations, which are simplified with the coupled-mode (nonlinear Dirac) equations.
Photonic band-gap crystals are periodic optical materials, spectrum of which consists of bands, separated
by band gaps. Periodic and nonlinear properties of the photonic crystals are modeled with the nonlinear
Maxwell equations, which are simplified with the coupled-mode (nonlinear Dirac) equations.
Coupled-mode equations are typically derived in the first band gap of the Bragg resonance between
two counter-propagating waves in low-contrast, weakly nonlinear photonic crystals. More complicated
wave resonance configurations were studied recently, with two oblique and four perpendicular waves.
The coupled-mode equations are formulated in bounded domains, subject to the radiation (transmission)
boundary conditions.
Using methods of separation of variables and generalized Fourier series, we study the stationary
transmission, reflection, and diffraction of resonant Bloch waves. Using dynamical system methods, we
classify stability of stationary solutions. With the finite-difference and spectral methods, we model
non-stationary dynamics of coupled resonant waves.
|
|