Many continuum problems arise in materials science and condensed matter physics, in particular the dynamics and equilibria of multiphase systems. These systems occur in various contexts: the mixed phase of a superconductor subjected to an external magnetic field, domain branching in micromagnetic materials, grain growth and coarsening in metallic alloys, and in eutectic solidification, for example. Mathematically, we employ "diffuse interface" models which then lead to critical points and gradient flows for Gibbs free energy functionals, Ginzburg-Landau systems, or phase-field models. These problems may be attacked using formal asymptotic expansions, methods of nonlinear analysis and partial differential equations, or numerical algorithms.

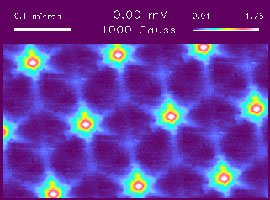
In high-temperature superconductivity, the continuum Ginzburg-Landau model is used to study macroscopic and mesoscopic superconductors and their in the magnetic properties, including vortices and flux penetration, Josephson junctions, and critical fields and currents. Of particular interest are the high critical temperature (Tc) superconductors (HTSC), since the nature of these compounds remains the object of intensive research in the condensed matter physics community.

J. Alberto Montero

• Recent preprint ...